Stochastic thermodynamics
Classical thermodynamics is applicable in a wide range of theoretical and practical systems. One of the key assumptions is, however, that the system is big and a large number of individual particles in involved. When the systems become smaller fluctuations play a crucial role. Examples for such systems range from biochemical networks and proteins to small particles immersed in a water bath. The framework of stochastic thermodynamics extends the notions of classical thermodynamics such as work, heat and entropy production to the level of individual trajectories. As a result derived quantities such as the efficiency can be defined in single particle systems, as for instance for molecular motors. Moreover, the fluctuations in the systems can be further characterized. For instance the fluctuation theorem relates the probabilities of trajectories with negative entropy production with the probability to observe a trajectory with positive entropy production
Mesoscopic heat engines
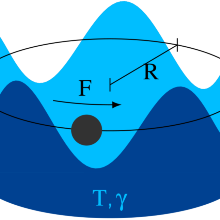
Ever since James Watt's steam engine, the urge to explore the fundamental principles governing the performance of devices that convert thermal energy into useful work was one of the major quests in thermodynamics. From a conceptual point of view, such heat engines can be divided into two classes. Cyclic engines use a reciprocating piston to generate mechanical work by periodically compressing and expanding a working fluid at varying temperature.
Thermoelectric engines consist of two heat and particle reservoirs, which are permanently coupled by a conductor. Due to the Seebeck effect, the heat current flowing naturally in this setup can drive a particle current into the same direction thus generating electrical power. During the last decades, substantial efforts have been gone into the miniaturization of both of these types of devices down to micro- and nanometers. On theses small scales, their operation principles can be scrutinized under the microscope by virtue of precise measurements of characteristic quantities like applied work or exchanged heat. Here, we use the framework of stochastic thermodynamics to investigate the laws that determine the efficiency and power of mesoscopic heat engines. In particular, we are interested in the relation between these two figures and the attainability of the Carnot efficiency, a universal upper bound following from the second law.
Related publications
- Periodic thermodynamics of open quantum systems, K. Brandner and U. Seifert, Phys. Rev. E 93, 062134 (2016), Abstract, Download
- Optimal performance of periodically driven, stochastic heat engines under limited control, M. Bauer, K. Brandner, and U. Seifert, Phys. Rev. E 93, 042112 (2016), Abstract, Download
- Thermodynamics of micro- and nano-systems driven by periodic temperature variations, K. Brandner, K. Saito, and U. Seifert, Phys. Rev. X 5, 031019 (2015), Abstract, Download
- Bound on thermoelectric power in a magnetic field within linear response, K. Brandner and U. Seifert, Phys. Rev. E 91, 012121 (2015), Abstract, Download
- Classical Nernst engine, J. Stark, K. Brandner, K. Saito, and U. Seifert, Phys. Rev. Lett. 112, 140601 (2014), Abstract, Download
- Multi-terminal thermoelectric transport in a magnetic field: Bounds on Onsager coefficients and efficiency, K. Brandner and U. Seifert, New J. Phys. 15, 105003 (2013), Abstract, Download
- Strong bounds on Onsager coefficients and efficiency for three terminal thermoelectric transport in a magnetic field, K. Brandner, K. Saito, and U. Seifert, Phys. Rev. Lett., 110, 070603 (2013), Abstract, Download, Viewpoint
Thermodynamics and information
The idea of using thermal fluctuations to extract useful work from a heat bath, thus creating an isothermal engine, is linked to the famous gedankenexperiments of Maxwell's demon (1867) and Szilard's engine (1929). In those experiments, a „demon“ extracts work cyclically from a heat bath by using the information acquired through the measurement of an adequate property - velocity or position - of the system. This apparent contradiction with the second law of thermodynamics was first resolved in 1967 by Rolf Landauer through his celebrated principle, which states that the erasure of a bit of information has a minimal energetic cost, thus linking thermodynamics to information theory. These concepts can nowadays be tested by experiments at the single-molecule level using the framework of stochastic thermodynamics. Our aim is to study theoretically systems for which one can convert information into work, e.g., by controlling the position of a Brownian particle in a laser trap or by implementing a periodic measurement and feedback. Moreover, we are interested in developing autonomous models for Maxwell's demon. With these models, we hope to shed light in issues that are not yet fully understood, as for example, the writing and erasure of information and the linear response theory.
Related publications
- Thermodynamic efficiency of learning a rule in neural networks, S. Goldt, and U. Seifert, New J. Phys. 19, 113001 (2017), Abstract, Download, Video abstract
- Stochastic thermodynamics of resetting, J. Fuchs, S. Goldt, and U. Seifert, EPL, 113, 60009 (2016), Abstract, Download
- Unifying three perspectives on information processing in stochastic thermodynamics, A. C. Barato, and U. Seifert
Phys. Rev. Lett. 112, 090601 (2014), Abstract, Download - Stochastic thermodynamics of bipartite systems: transfer entropy inequalities and a Maxwell's demon interpretation, D. Hartich, A. C. Barato, and U. Seifert, J. Stat. Mech., P02016 (2014), Abstract, Download
- Rate of mutual information between coarse-grained non-Markovian variables, A. C. Barato, D. Hartich, and U. Seifert
J. Stat. Phys. 153, 460-478 (2013), Abstract, Download - An autonomous and reversible Maxwell's demon, A. C. Barato, and U. Seifert, EPL, 101, 60001 (2013), Abstract, Download
- Efficiency of a Brownian information machine, M. Bauer, D. Abreu, and U. Seifert, J. Phys. A: Math. Theor. 45, 162001 (2012), Abstract, Download
- Thermodynamics of genuine non-equilibrium states under feedback control, D. Abreu, and U. Seifert, Phys. Rev. Lett. 108, 030601 (2012), Abstract, Download
- Extracting work from a single heat bath through feedback, D. Abreu and U. Seifert, EPL 94, 10001 (2011), Abstract, Download
Hidden degrees of freedom
Most physical descriptions involve some sort of coarse graining. Particulary in the description of meso or macroscopic systems one needs to deal with hidden fast degrees of freedom such as the myriads of solvent particles that are treated in an effective manner when describing the diffusion of a colloidal particle in the Langevin approach. Generally, an effective description of such unobserved degrees of freedom is justified if there is a clear-cut time-scale separation in the dynamics. Without such a time-scale separation, neglecting hidden slow degrees of freedom naively can lead to inconsistencies. Here, we investigate the role of hidden slow degrees of freedom in the fluctuation theorem for the apparent entropy production one would infer from a reduced set of variables.
Related publications
- Role of hidden slow degrees of freedom in the fluctuation theorem, J. Mehl, B. Lander, C. Bechinger, V. Blickle, and U. Seifert, Phys. Rev. Lett. 108, 220601 (2012), Abstract, Download
- Can one identify non-equilibrium in a three state system by analyzing two-state trajectories?, C. Amann, T. Schmiedl, and U. Seifert, J. Chem. Phys. 132, 041102 (2010), Abstract, Download
Efficiency of nanomachines
Molecular motors as well as the recently developed artificial nanomachines inspired by them operate in an aqueous solution of constant temperature. In contrast with heat engines limited by Carnot’s law, thermodynamics constrains their efficiency by 1. Like for heat engines, however, operating at the upper bound comes at the price of zero power since it requires infinitely slow driving. A practically more relevant question then is about efficiency at maximum power which we have analyzed for autonomous soft nanomachines using a quite general approach requiring minimal assumptions.
Related publications
- Universal trade-off between power, efficiency and constancy in steady-state heat engines, P. Pietzonka, and U. Seifert, Phys. Rev. Lett. 120, 190602 (2018), Abstract, Download
- Efficiency of autonomous soft nano-machines at maximum power, U. Seifert, Phys. Rev. Lett. 106, 020601 (2011), Abstract, Download
- Stochastic thermodynamics of single enzymes and molecular motors, U. Seifert, Eur. Phys. J. E 34, 26 (2011), Abstract, Download
- Efficiency at maximum power: An analytically solvable model for stochastic heat engines, T. Schmiedl, and U. Seifert
EPL 81, 20003 (2008), Abstract, Download, Experimental realization